반응형
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- 정보처리기사실기정리
- 국비IT
- CSS
- php
- 평일코딩
- 자바스크립트 코딩테스트
- 코딩테스트
- 자스코테
- 정보처리기사실기
- 정보처리기사
- 오라클
- javascript
- 정보처리기사요약
- Java의정석
- 정보처리기사실기요약
- typescript
- react
- spring
- 타입스크립트
- 자바스크립트
- 이안의평일코딩
- 스프링
- Oracle
- 자바의정석
- VUE
- ReactNative
- 정보처리기사정리
- 국비코딩
- 리액트네이티브
- 리액트
Archives
- Today
- Total
이안의 평일코딩
그래프 3) 인접행렬과 인접리스트의 차이 본문
반응형

그래프는 인접행렬(adjacency matrix) 혹은 인접리스트(adjacency list)로 표현한다.
노드 갯수가 적을 때는 인접행렬로도 충분하지만 노드 수가 많아지면 인접리스트를 이용하는게 효율이 좋다. (시간복잡도가 훨씬 줄어든다.)
인접행렬은 node와 edge의 정보를 행렬로 표현하는 방법으로, edge와 상관없이 모든 node를 표현해야 하기 때문에 node의 수가 많을수록 메모리 사용량이 늘어난다. (node의 개수만큼 반복문을 돌아야 하기 때문)
인접리스트는 node와 edge의 정보를 리스트로 표현하는 방법으로, 연결된 것만 표시하므로 인접행렬에 비해 간단하다.
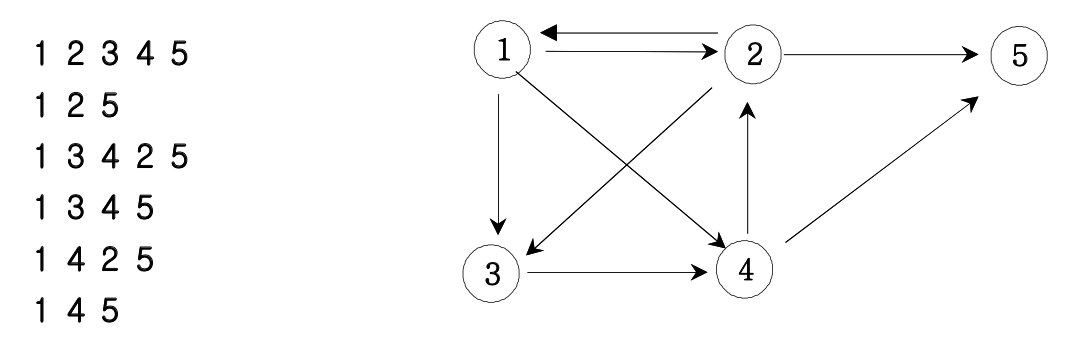
// 인접행렬
function solution(n, arr) {
let answer = 0;
let graph = Array.from(Array(n + 1), () => Array(n + 1).fill(0));
let ch = Array.from({ length: n + 1 }, () => 0); // check 배열
/*
[0, 0, 0, 0, 0, 0]
*/
for (let [a, b] of arr) { // arr 값 1개 씩 탐색
graph[a][b] = 1; // 방향 그래프에서 graph arr 에 1로 체크
}
function DFS(v) {
if (v === n) { // n 마지막 노드 도착시 answer++
answer++;
/*
[1, 2, 3, 4, 5]
[1, 2, 5]
[1, 3, 4, 2, 5]
[1, 3, 4, 5]
[1, 4, 2, 5]
[1, 4, 5]
*/
} else {
for (let i = 1; i <= n; i++) {
if (graph[v][i] === 1 && ch[i] === 0) {
// 1이면 갈수있고, ch가 0이면 간적이 없음
ch[i] = 1; // 지나갔으면 1로
DFS(i); // 다음 번호 for loop
ch[i] = 0; // back전에 다시 0 초기화
}
}
}
}
ch[1] = 1; // 출발점 1 (없으면 1로 돌아가기 때문)
DFS(1);
return answer;
}
let arr = [[1, 2],[1, 3],[1, 4],[2, 1],[2, 3],[2, 5],[3, 4],[4, 2],[4, 5]];
console.log(solution(5, arr));// 인접리스트
function solution(n, arr) {
let answer = 0;
let graph = Array.from(Array(n + 1), () => Array());
let ch = Array.from({ length: n + 1 }, () => 0);
for (let [a, b] of arr) {
graph[a].push(b); // 인접 리스트
}
function DFS(v) {
if (v === n) {
answer++;
/*
[1, 2, 3, 4, 5]
[1, 2, 5]
[1, 3, 4, 2, 5]
[1, 3, 4, 5]
[1, 4, 2, 5]
[1, 4, 5]
*/
} else {
for (let i = 0; i <= graph[v].length; i++) {
// 그래프 행의 길이만큼 for loop
if (ch[graph[v][i]] === 0) {
// 체크 유무 따짐
ch[graph[v][i]] = 1;
DFS(graph[v][i]); // graph[v][i]는 정점
ch[graph[v][i]] = 0;
}
}
}
}
ch[1] = 1;
DFS(1);
return answer;
}
let arr = [[1, 2],[1, 3],[1, 4],[2, 1],[2, 3],[2, 5],[3, 4],[4, 2],[4, 5]];
console.log(solution(5, arr));
문제풀이에서 보듯 둘의 차이는 먼저 인접행렬에서는 0으로 채운 배열을 인접리스트에서는 빈 배열을 생성한 뒤,
행렬은 a에서 b로 갈 수 있는 길을 1로 채워주고 리스트는 갈 수 있는 길을 리스트로 만들어 준다.
// 인접행렬
let graph = Array.from(Array(n + 1), () => Array(n + 1).fill(0));
/*
0: (6) [0, 0, 0, 0, 0, 0]
1: (6) [0, 0, 0, 0, 0, 0]
2: (6) [0, 0, 0, 0, 0, 0]
3: (6) [0, 0, 0, 0, 0, 0]
4: (6) [0, 0, 0, 0, 0, 0]
5: (6) [0, 0, 0, 0, 0, 0]
*/
for (let [a, b] of arr) {
graph[a][b] = 1;
}
//console.log(graph)
/* 1 2 3 4 5
0: (6) [0, 0, 0, 0, 0, 0]
1: (6) [0, 0, 1, 1, 1, 0]
2: (6) [0, 1, 0, 1, 0, 1]
3: (6) [0, 0, 0, 0, 1, 0]
4: (6) [0, 0, 1, 0, 0, 1]
5: (6) [0, 0, 0, 0, 0, 0]
*/
/////////////////////////////////////////////////////////////////////
// 인접리스트
let graph = Array.from(Array(n + 1), () => Array());
/*
0: []
1: []
2: []
3: []
4: []
5: []
*/
for (let [a, b] of arr) {
graph[a].push(b);
}
// console.log(graph)
/*
0: []
1: [2, 3, 4]
2: [1, 3, 5]
3: [4]
4: [2, 5]
5: []
*/
그리고 DFS 함수 안에서의 반복문과 조건문도 달라진다.
인접행렬은 i가 n까지 돌지만 인접리스트에서 i는 각 리스트의 길이만큼 돈다.
행렬은 1이고 체크가 없을때 이동이 가능하지만 리스트에서는 가능한 것만 있기 때문에 체크유무만 확인한다.
행렬은 i번째 체크를 확인하고 리스트는 리스트의 정점의 체크를 확인하고 DFS를 돌린다.
// 인접행렬
for (let i = 1; i <= n; i++) {
if (graph[v][i] === 1 && ch[i] === 0) {
// 1이면 갈수있고, ch가 0이면 간적이 없음
ch[i] = 1;
DFS(i); // 다음 번호 for loop
ch[i] = 0;
}
}
///////////////////////////////////////////////
// 인접리스트
for (let i = 0; i <= graph[v].length; i++) {
if (ch[graph[v][i]] === 0) {
// 체크 유무 따짐
ch[graph[v][i]] = 1;
DFS(graph[v][i]); // graph[v][i]는 정점
ch[graph[v][i]] = 0;
}
}반응형
'Study > JS Algorithm Rocket' 카테고리의 다른 글
| 그래프 4) DFS와 BFS의 차이 (0) | 2021.12.03 |
|---|---|
| 그래프 2) 방향 그래프, 무방향 그래프, 가중치 방향그래프 정리 (0) | 2021.12.01 |
| 그래프 1) binary tree, vertex, node, edge 용어 정리 (0) | 2021.12.01 |
| [JS] 재귀함수 알고리즘 (스택프레임) (0) | 2021.11.08 |
| [자료구조(스택, 큐)] 크레인 인형뽑기 (카카오 기출) (0) | 2021.10.06 |
Comments




